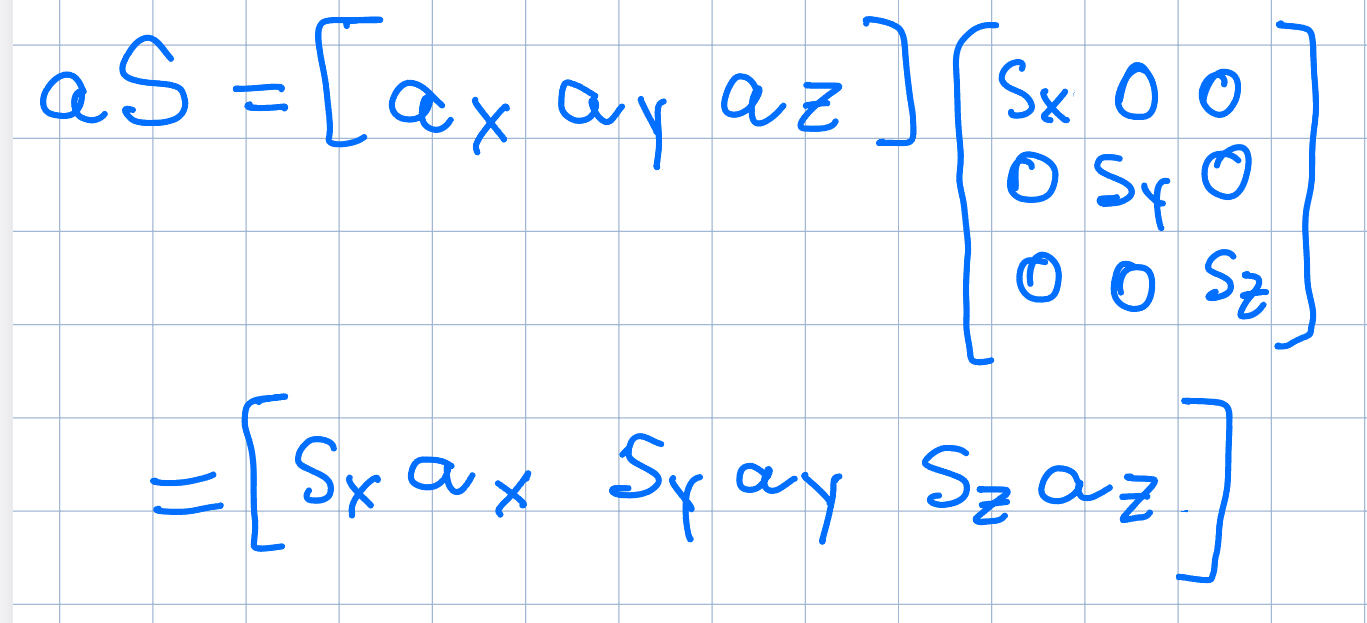Introduction to 3D math for games - Part 1
Start learning about vectors and how they are used in game engines
Hello and welcome to Game Engine Tutorials! A game is a mathematical model of a virtual world simulated in real time. Game engines make use of virtually all branches of mathematics, from trigonometry to algebra to statistics to calculus. 3D vector and matrix math are the most common operations in game programming.
This post is an overview of the mathematical tools needed by a typical game programmer. Specific topics will be covered in the next articles, so don’t forget to subscribe in the link below :)
Solving 3D problems in 2D
Sometimes we can solve a 3D vector problem by drawing pictures in 2D (way easier to do). The equivalence between 2D and 3D does not work all the time. For example, the cross-product operation is only defined in 3D. Some problems only make sense when all three dimensions are considered.
You can start thinking of how to solve a 3D problem in 2D - a simplified version of the problem in 2D. Once you understand how it works in 2D, you can extend to the three dimensions.
Points and Vectors
Most modern 3D games are made up of three-dimensional objects in a virtual world. The game engine needs to keep track of all positions, orientations and scales of all these objects, animate them, and transform into screen space to be rendered on screen. 3D objects are almost always made up of triangles, vertices of which are represented by points.
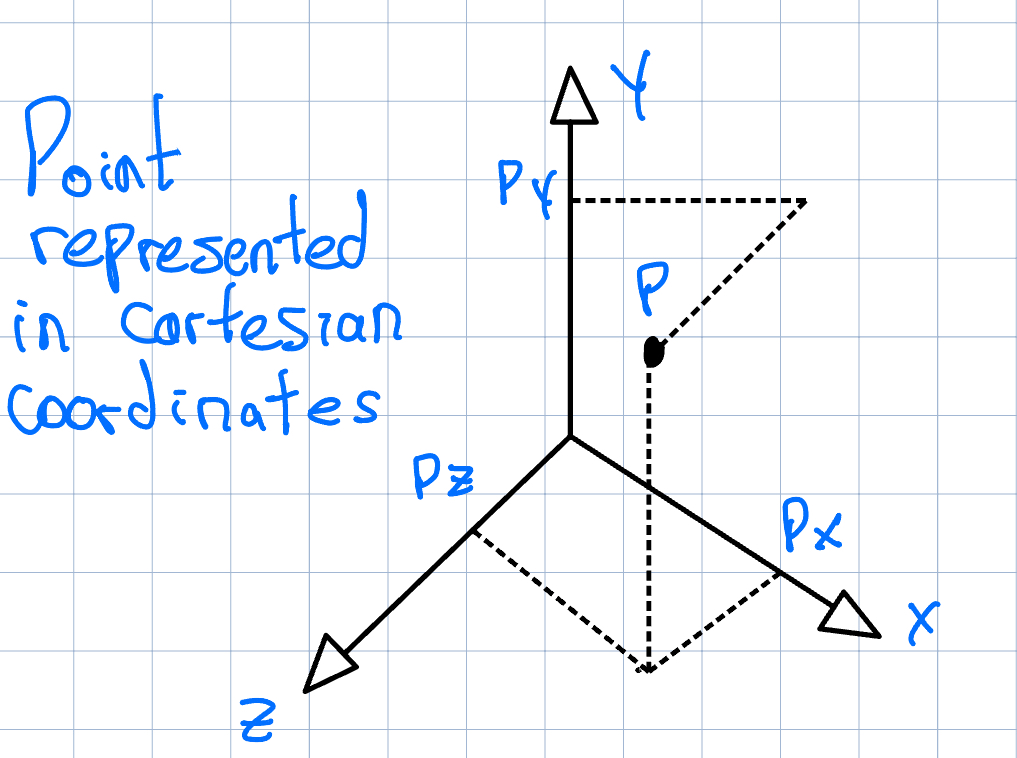
A point is a location in n-dimensional space (in games, n is usually equal to 2 or 3). The Cartesian system uses two or three mutually perpendicular axes to specify a position in 2D or 3D space. A point P is represented by a pair of triple of real numbers, (Px and Py) or (Px, Py, Pz).
Representation of a point P in the Cartesian system (drawn by me, not to scale):
There are other systems like the cylindrical coordinates and spherical coordinates systems. We must choose the system that best maps to the problem at hand.
For example, we would employ the cylindrical coordinates system in a racing game where the track is a large, ascending spiral, similar to a multi-level parking garage. The position of the cars on the track can be easily described using radial distance from the center (radius), the angular position around the center (theta), and the height above the base (z).
When a car moves around the spiral, its movement in the radial and angular directions can be more easily calculated and controlled in cylindrical coordinates. Steering the car around the track primarily involves changing the angular component, while moving up or down the spiral changes the z-component.
Here’s a game scenario with a spiral track generated by DALL-E. This visual helps in understanding how a cylindrical coordinate system can be effectively used in such a game design.
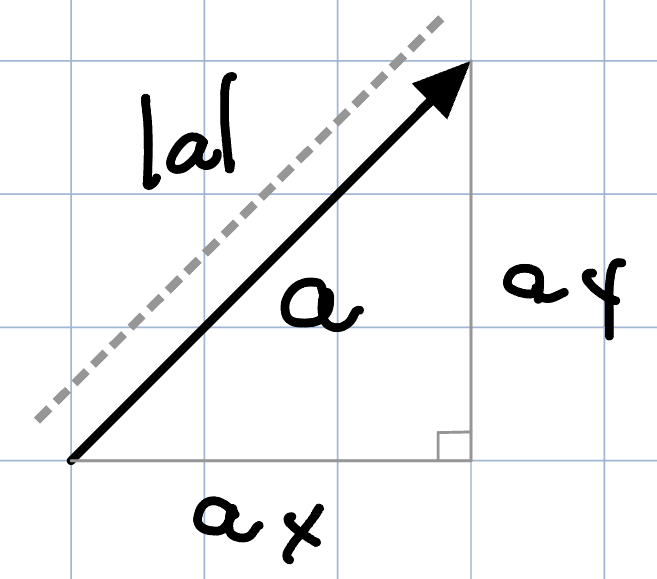
Vector
A vector is a quantity that has both a magnitude and direction in n-dimensional space. It can be visualized as a directed line segment from a point called the tail to a point called the head. A scalar, on the other hand, represents a magnitude but has no direction.
A 3D vector can be represented by a triple of scalars (x, y, z), just as a point can be. Technically, a vector is an offset to some known point. It can be moved anywhere in 3D space - as long as its magnitude and direction don’t change, it’s the same vector.
A vector can be used to represent a point once we fix its tail to the origin of our coordinate system. Such a vector is often called a position vector or radius vector.
Cartesian Basis Vectors
It’s often useful to define three orthogonal unit vectors (vectors that are mutually perpendicular and each with a length equal to one), corresponding to the three principal cartesian axes.
The unit vector along with the x-axis is typically called i, the y-axis unit vector is called j, and the z-axis unit vector is called k. The vectors i, j and k are sometimes called cartesian basis vectors.
Any point or vector can be expressed as a sum of scalars (real numbers) multiplied by these unit basis vectors.
For example: (5, 3, -2) = 5i + 3j - 2k
Vector example in C++:
In the following example, the Vector3D class represents a 3D vector with x, y, and z components. The class includes a method to calculate the vector's magnitude, overloads the + operator for vector addition, and the * operator for scalar multiplication. The main function demonstrates creating vectors, adding them, scaling a vector, and displaying their properties.
#include <iostream>
#include <cmath>
class Vector3D {
public:
float x, y, z;
// Constructor to initialize the vector
Vector3D(float x, float y, float z) : x(x), y(y), z(z) {}
// Compute the magnitude of the vector
float magnitude() const {
return std::sqrt(x * x + y * y + z * z);
}
// Operator overloading for vector addition
Vector3D operator+(const Vector3D& v) const {
return Vector3D(x + v.x, y + v.y, z + v.z);
}
// Operator overloading for scalar multiplication
Vector3D operator*(float scalar) const {
return Vector3D(x * scalar, y * scalar, z * scalar);
}
// Display the vector
void display() const {
std::cout << "Vector(" << x << ", " << y << ", " << z << ")" << std::endl;
}
};
int main() {
// Creating two 3D vectors
Vector3D v1(1.0, 2.0, 3.0);
Vector3D v2(4.0, 5.0, 6.0);
// Vector addition
Vector3D v3 = v1 + v2;
// Scalar multiplication
Vector3D v4 = v1 * 2.0;
// Displaying the vectors and their properties
std::cout << "Vector v1: ";
v1.display();
std::cout << "Vector v2: ";
v2.display();
std::cout << "Vector v3 (v1 + v2): ";
v3.display();
std::cout << "Vector v4 (v1 * 2): ";
v4.display();
std::cout << "Magnitude of v1: " << v1.magnitude() << std::endl;
return 0;
Vector operations
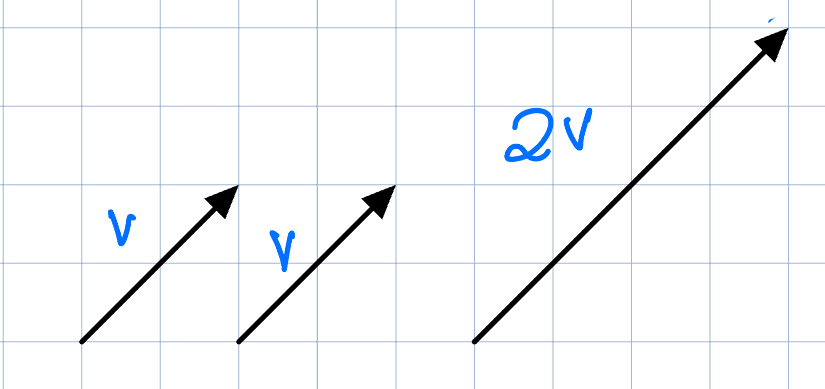
Multiplication of a vector by the scalar 2:
The multiplication of a vector a by a scalar s is done by multiplying the individual components of a by s:
sa = (sax, say, saz)
Any multiplication by a scalar has the effect of scaling the magnitude of the vector, while leaving its direction unchanged. Multiplication by -1 will flip the direction of the vector (the head becomes the tail and vice versa).
We should also address nonuniform scale - the scale factor can be different along each axis.
s ⦻ a = (sax, syay, szaz)
This is another way of writing that equation:
Addition and subtraction
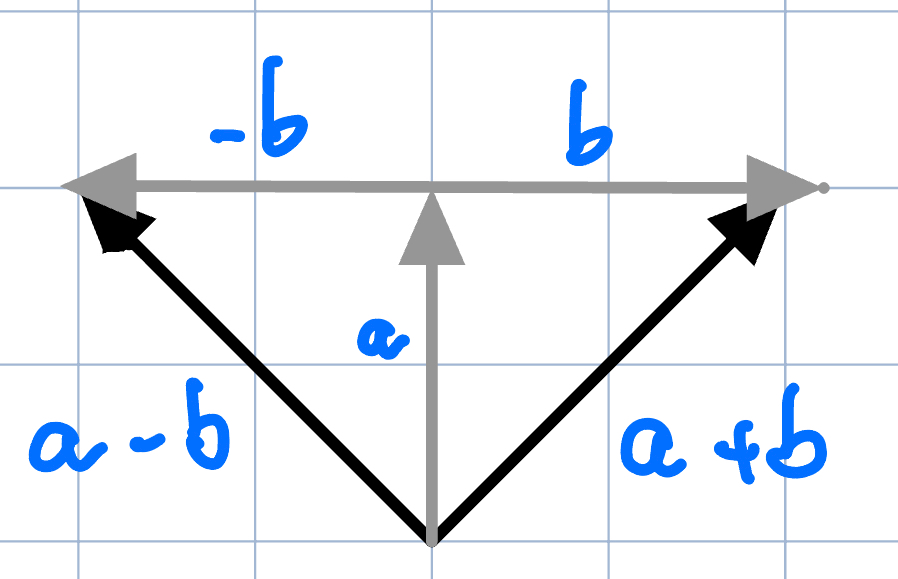
The addition of two vectors an and b is defined as the vector whose components are the sums of the components of an and b. This can be visualized by placing the head of vector a onto the tail of vector b - the sum is then the vector from the tail of a to the head of b:
a + b = [(ax + bx), (ay + by), (az + bz)]
Vector subtraction a-b is nothing more than addition of an and -b (the result of scaling b by -1, which flips it around).
a - b = [(ax - bx), (ay - by), (az-bz)]
Vector addition and subtraction:
Magnitude of vector:
Okay, that’s a good start! In part 2, we’ll dive deep in vector operations like dot product and projection, matrices and transformations. Don’t forget to subscribe!
Also, have you ever thought about becoming a writer? I’d highly recommend starting a Subatack blog: