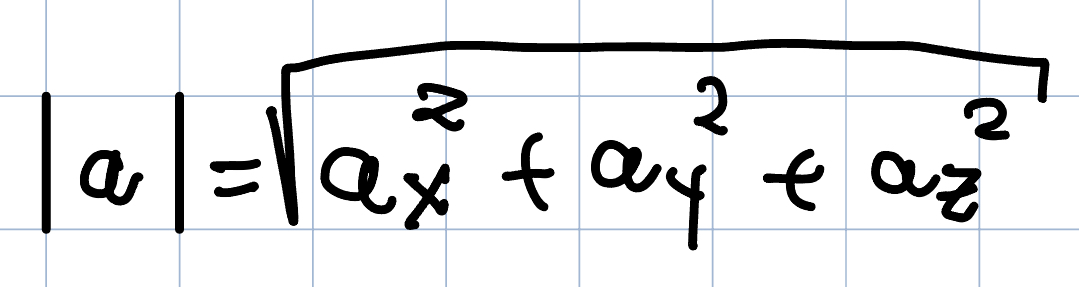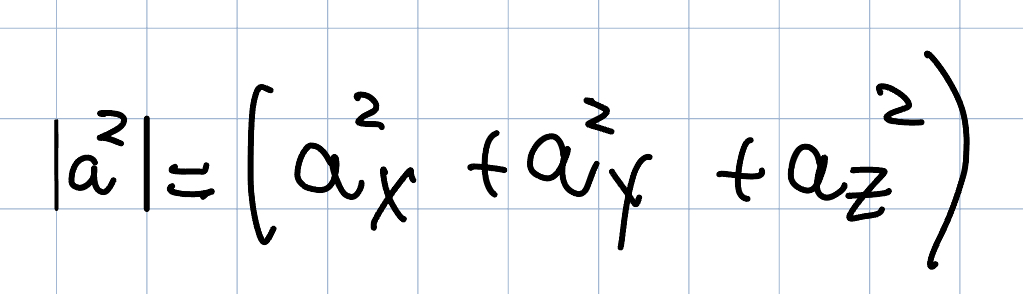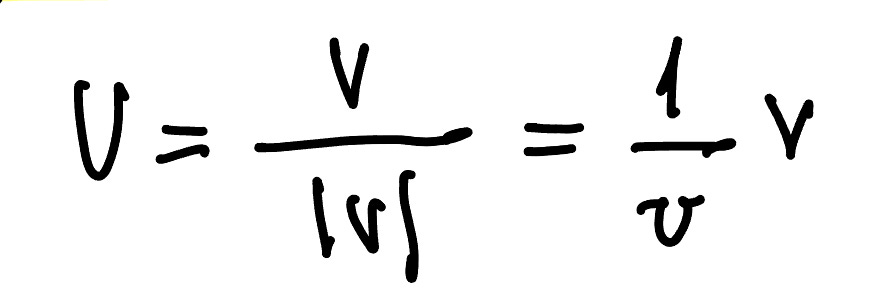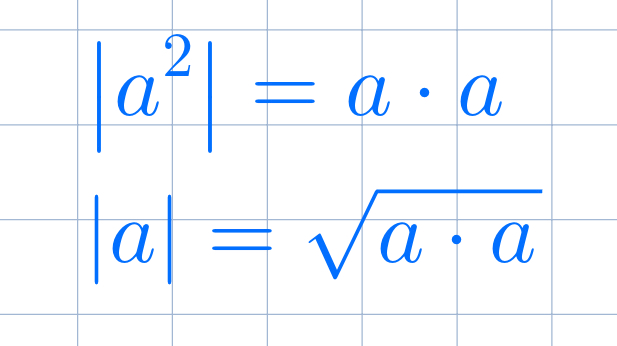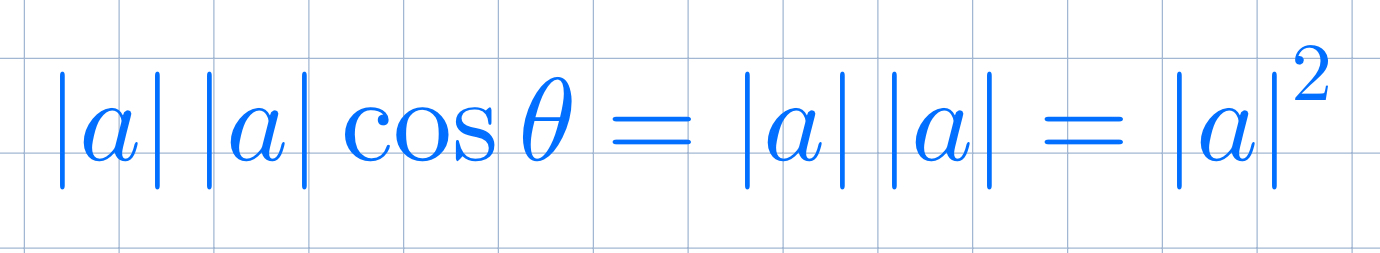Introduction to 3D math for games - Part 2

This is the Part 2 of our 3D math for games introduction and we have to go through more vector operations, types of vectors and dot product.

Hello and welcome to Game Engine Tutorials! This is the Part 2 of our 3D math for games introduction and we have to go through more vector operations, types of vectors and dot product.

Game engine programming is not hard, but challenging. Once you have all the main physical concepts on your mind, you’ll be able to play around easily with the code.

Magnitude

Magnitude of a vector is a scalar representing the length of the vector as it would be measured in 2D or 3D space. It’s denoted by placing vertical bars around the vector’s boldface symbol. We can use a Pythagorean theorem to calculate a vector’s magnitude:

Vector Operations

If you read Part 1, you can already solve all sorts of game problems with the vector operation you’ve learned so far. Operations like addition, subtraction, scaling, and magnitude are used to generate new data out of the things we already know.

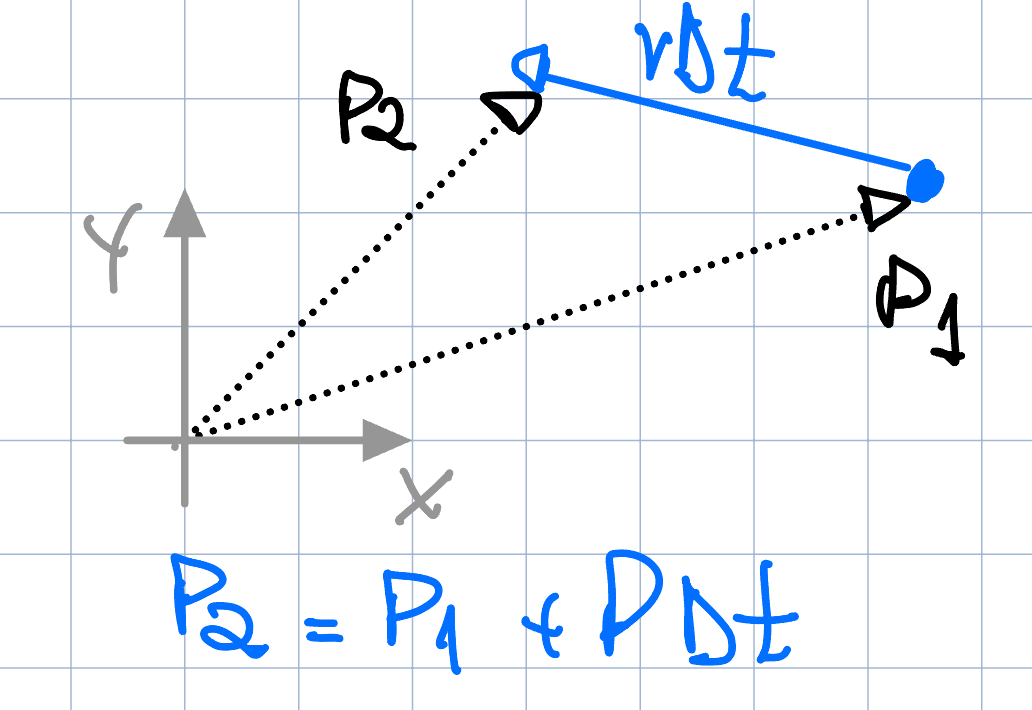
If we have the current position vector of an AI character P1, and a vector v representing its current velocity, we can find its position on the next frame P2 by scaling the velocity vector by the frame time interval DeltaT, and then adding it to the current position:

P2 = P1 + PDeltaT , this is known as explicit Euler integration - it’s valid when the velocity is constant.

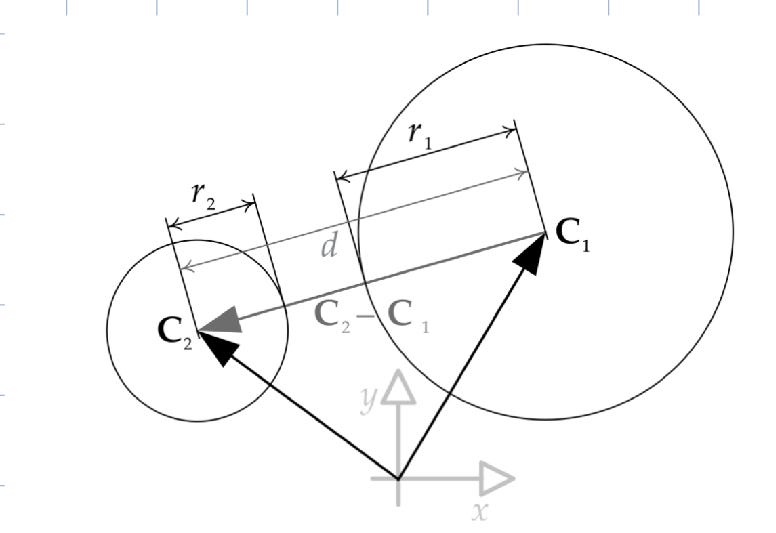
Also, let’s say we’ve got two spheres, and we want to know if they intersect. If we know the center points of the two spheres, C1 and C2, we can find a direction vector between them by simply subtracting the points, d = C2 - C1. The magnitude of this vector is D = |d| determines how far apart the spheres' centers are. If this distance is less than the sum of the spheres’ radii, they are intersecting otherwise they are not.

A sphere-sphere intersection test involves only vector subtraction, vector magnitude and floating-point comparison operations.

Square roots are expensive to calculate, so game programmers should always use squared magnitude whenever it’s valid to do so.

Using the squared magnitude is valid when comparing the relative lengths of two vectors (is a vector a longer than vector b?) , or when comparing a vector’s magnitude to some other (squared) scalar quantity.

Normalization and Unit vectors

A unit vector is a vector with a magnitude (length) of one. Unit vectors are useful in 3D mathematics and game programming.

Given an arbitrary vector v of length v = |v|, we can convert it to a unit vector u in the same direction as v, but has unit length. We simply multiply v by the reciprocal of its magnitude. We call this normalization:

Normal Vectors

A vector is normal to a surface if it’s perpendicular to that surface. Normal vectors are highly useful in games and computer graphics. A plane can be defined by a point and a normal vector. In 3D graphics, lighting calculations make heavy use of normal vectors to define the direction of surfaces relative to the direction of the light rays impinging upon them.

Normal vectors are usually of unit length, but they do not need to be. A normalized vector is any vector of unit length. A normal vector is any vector that is perpendicular to a surface, whether or not it is of unit length.

Dot Product and Projection

Vectors can be multiplied, but unlike scalars there are a number of different kinds of vector multiplication. In game programming, we most often work with the following two kinds of multiplication:

• The dot product (scalar product or inner product), and

• the cross product (vector product or outer product)

Take a look at this hand-written explanation:

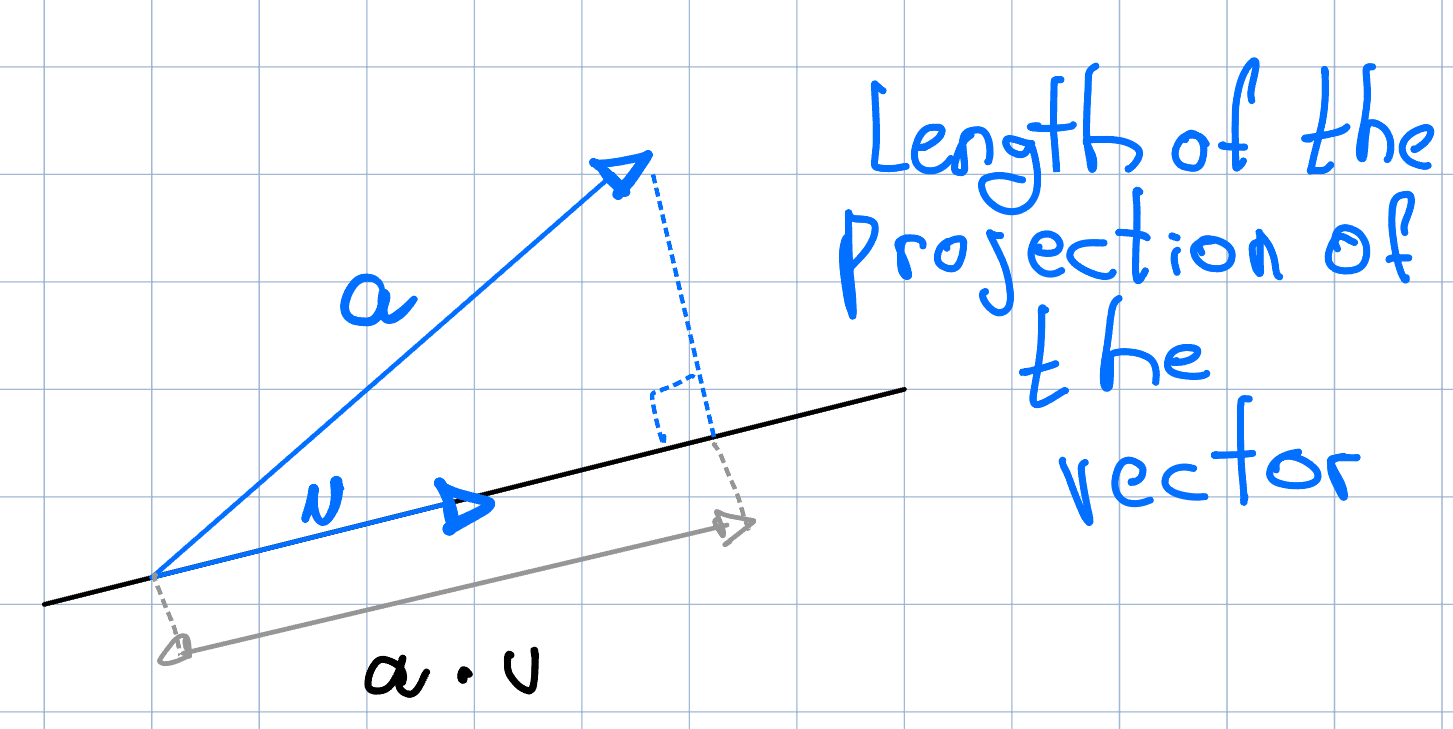
Vector Projection

If u is a unit vector (|u| = 1), then the dot product (a . u) represents the length of the projection of a vector an onto the infinite line defined by the direction of u. This projection concept works well in 2D or 3D and is highly useful for solving a wide variety of three-dimensional problems

Magnitude as a dot product

The squared magnitude of a vector can be found by taking the dot product of that vector with itself. Its magnitude is then easily found by taking the square root:

This works because the cosine of zero degrees is 1, so:

Dot products are great for testing if two vectors are collinear or perpendicular, or whether they point in roughly the same or roughly opposite directions. For any two arbitrary vectors a and b, game programmers often use the following tests:

• Collinear. (a •b) = |a||b| = ab (i.e., the angle between them is exactly O degrees-this dot product equals +1 when a and b are unit vectors).

• Collinear but opposite. (a • b) = -ab (i.e., the angle between them is 180 degrees-this dot product equals -1 when a and b are unit vectors).

• Perpendicular. (a • b) = 0 (i.e., the angle between them is 90 degrees).

• Same direction. (a • b) > 0 (i.e., the angle between them is less than 90 degrees).

• Opposite direction. (a • b) < 0 (i.e., the angle between them is greater

Okay! In Part 3, we’ll be talking about Cross Product! Enjoy and don’t forget to subscribe for free!